Bollard Pull Calculations for Towing Operations – an Introduction
Part I – Calculating the required Bollard Pull (BP)
SECTION A – INTRODUCTION
Bollard Pull calculation is one of the most frequent calculations performed in marine towing operations.
Towing operations involve the pulling of a vessel (it can be a barge, ship or an offshore structure) using another vessel (usually a tug).
From a very basic point of view, we can draw the following conclusions regarding towing
- A bigger vessel will require higher force for towing
- The harsher the environment, the more will be the towing force required
- The efficiency of the tug deployed for towing will also affect the towing operation
When selecting and deploying tugs for towing operations, we would like to know a few things before we make a final decision:
- How big a tug should I select for safely towing the vessel?
- How much maximum speed will I be able to make with the tug(s) I selected?
Each of the above questions merits a detailed explanation, and we will cover each of them separately. In this Article, we will cover the first question – how big a tug is required for safe towing of a vessel?
First, let’s clear some basic concepts. Please note that this article covers only the scenario of head sea towing.
SECTION B – BASIC CONCEPTS
Concept – Bollard Pull of a Tug

Source: weir-jones.com
The capacity of tugs is measured by their rated Bollard Pull. The Bollard Pull of a tug is the force it exerts at zero forward speed, in calm water conditions, with the engine working at its full power (100% MCR). Continuous Bollard Pull (CBP) is measured by a test as the average bollard pull measured at a length of time (say 10 minutes), while Maximum Bollard Pull is the highest bollard pull measured during the test.
Concept – Towing Efficiency and available pulling force at zero speed
Source: pixabay
The tug has an efficiency of its own when towing the vessel in sea. It depends on the environment of the tow, and on size of the vessel towed.
If the bollard pull of a tug is denoted by BP, and its towing efficiency is denoted by ƞ, then the total available pulling force from the tug will be
Available pulling force of the tug = Bollard Pull of the tug x Towing efficiency
Available Pulling force of the tug = BP x ƞ
Concept – Required Towing Force
How do we relate the Bollard Pull of the tug to the vessel being towed?
Basically, the vessel being towed will experience environmental forces of wind, wave and current in the sea. Together, these forces constitute the ‘Towing force’. Let’s denote it by FTOT
For the tug to be able to pull the vessel, the available pulling force of the Tug must be greater than the total force on the vessel.
- BP x ƞ > FTOT
- BP > FTOT/ ƞ
Thus the Bollard Pull of the tug should be more than FTOT/ ƞ. This is called the Required Bollard Pull, and this is what we seek to calculate. Next we will see how the towing force can be calculated.
Concept – Environmental forces
The required Towing force is defined as the force which is required to HOLD the vessel in sea under certain environmental conditions of wind, wave and current.

Total Towing Force, FTOT = Wind Force + Wave force + Current force
Please note that the towing force is the required force for HOLDING the vessel (also called STALL condition), and not for towing it.
Now, what are these environmental conditions and where do we get them from?
When towed in the sea, a vessel will experience forces of wind, wave and current. To HOLD the vessel in the given environment, we need to overcome these forces.
- Wind force acts on the part of the vessel above waterline and exposed to wind
- Current force acts on the underwater portion of the vessel
- Wave forces – the waves coming on to the vessel add to the resistance force on the vessel
Wind forces depend on the wind speed, current forces depend on the current speed and Wave forces depend on the (significant) height of waves.
Industry standards like DNVGL Guidelines for Marine Transportation (earlier ND-0030, now superseded by DNVGL-ST-N001) prescribe the standard wind, wave and current parameters to be used for bollard pull calculations, depending on condition under which the towing is being performed.
ND-0030 requires that the bollard pull of the tug should be sufficient to HOLD the towed vessel in the environment stated below:
Standard Criteria – For Open Ocean tows, following environmental parameters are prescribed as per ND-0030
- Wind Speed – 20 m/s (roughly 40 knots)
- Current speed – 0.5 m/s (roughly 1 knot)
- Significant Wave Height – 5 meters
For benign weather areas, the following criteria are prescribed as per ND0030
- Wind Speed – 15 m/s (roughly 30 knots)
- Current speed – 0.5 m/s (roughly 1 knot)
- Significant Wave Height – 2 meters
A question naturally arises – how do we know if the tow is an open ocean tow or a benign tow? For this we need to study the environment of the route of the tow, and get the historical environment data of the route. We can get it from environment data provider like Metocean. In some cases, data from Nautical charts is also acceptable (depends on the discretion of Marine Warranty Surveyor). The wind speed, wave height and current speed should be obtained for the specific time of the year when the tow is expected to take place. For example, if the towing operation is expected in May +/- 2 months, then the environment data from March till July should be referenced. The most extreme values for the period should be utilized.
From the environment data, we can decide whether it is an open ocean tow or a benign tow. Basically, if anywhere along the route a wave of (significant) height more than 2 meters is expected, then the Open Ocean criteria is to be used. If everywhere along the route, waves of significant wave height less than 2 meters are expected, then the environment data must be submitted to the Warranty Surveyor and exemption obtained for using the ‘benign’ sea state case before proceeding with Bollard Pull calculations.
SECTION C – CALCULATION STEPS

Now we can delineate the steps for performing Required Bollard Pull calculations for towing a vessel as follows:
- Step 1 – Determine the environmental parameters (Open Ocean or Benign)
- Step 2 – Calculate the Wind, Wave and Current forces on the vessel
- Step 3 – Add up the wind, wave and current forces to find the total force on the vessel, FTOT
- Step 4 – Get the towing efficiency of the tug, ƞ
- Step 5 – Calculate the minimum required Bollard Pull (BP) using the formula
Minimum Required BP > FTOT/ ƞ
Now we will discuss the calculation methods in detail.
SECTION D – CALCULATION METHODS IN DETAIL

Wind forces
Wind forces are the forces on the part of the vessel above the waterline which is exposed to winds.
For calculating wind force, besides the wind speed and air density, we need the Transverse wind-exposed sectional area of the vessel (also called windage area)
Calculating the transverse windage area
When the vessel is being towed forward, then the transverse section of the vessel faces the winds head on.
Some points to keep in mind when calculating this transverse windage area are:
- There are two parts of the windage area – the area contributed by the part of the vessel’s hull above water, and the area contributed by items on the deck, i.e., Cargo, Deck structures and Accommodation
- The area contributed by the hull can be obtained from the midship section dimensions/drawing
- The area contributed by above-deck items can be calculated as the area of the silhouette of the above deck items.
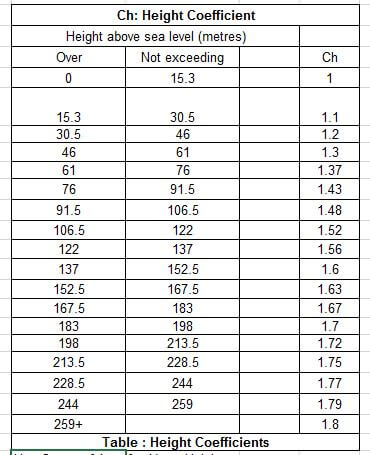
- Cargo height coefficient – The speed of wind varies with the height above the water surface. For zones of the cargo which are higher, a cargo height coefficient needs to be additionally applied to take into account the higher wind speeds experienced by higher zones of the cargo. Cargo height coefficients are provided in ABS MODU Rules (see below)
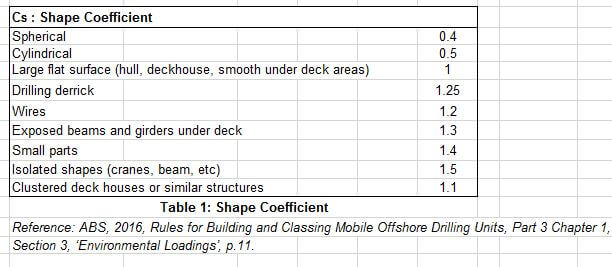
- Cargo shape coefficient – The wind force experienced by the cargo also depends on the shape of the cargo. For example, a box shaped cargo will experience higher forces than cargo which is cylindrical in shape (with the cylindrical face exposed to wind). To take into account the effect of cargo shape on wind force, a cargo shape coefficient needs to be incorporated in the windage area calculations. Cargo shape coefficients for typical cargo shapes are provided in ABS MODU Rules (see below)
- The final windage area should incorporate the height and shape coefficients
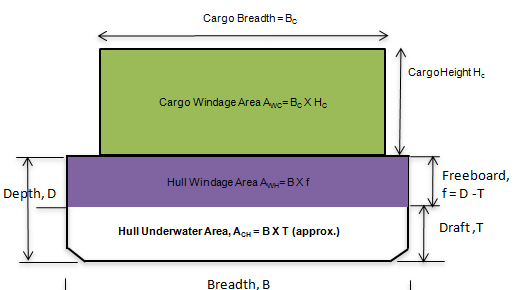
Sketch showing the Transverse Windage Area and Transverse Underwater Areas of a simple Barge
The wind force is calculated from the air density, wind speed and the transverse windage area using standard formula
Force = ½ x air density x (wind speed)2 x Transverse Windage Area
Current forces
The current forces are basically, the forces experienced by the underwater part of the hull.
The underwater part of the hull experiences what is called as ‘calm water resistance’. This is the resistance the ship experiences when it is moving in water without waves.
In the STALL scenario when the tow is not moving, the vessel is actually static, but the current moving against the vessel creates the same effect as the vessel moving with the speed of the current in calm water. Thus, the resistance experienced by the vessel because of current is equivalent to the resistance which the vessel will experience in calm water when moving at the speed of the current.
The Calm Water Resistance has many components, and is a complicated calculation. Calm water resistance of a ship can be calculated using
- Empirical methods like Holtrop-Mennen method, Taylor’s method etc. Each method is applicable to certain ship types
- Direct Model Tests
- Computer simulation
Barges
For barges, some studies have been done to develop empirical methods of calculating resistance. Some of them are
- Bureau Veritas – Towage at Sea of Vessels or Floating Units
- Offshore Technology Conference (OTC) Paper 3320 – Resistance of Offshore Barges and Required Horsepower
If the vessel is a barge, sometimes a simplification is adopted, subject to acceptance by MWS. Similar to the calculation of transverse wind force, the current force can also be calculated from the transverse underwater area.
Calculation of transverse underwater hull area is pretty simple in case of barges, which generally have a rectangular section shape. If the width of the Barge is B, and its draft is T, then the underwater transverse section area is simply B x T. If there are cuts around the bilge of the barge, these can be deducted from the area. The current force is finally calculated using the standard formula
Current force = ½ x water density x (current speed)2 x underwater transverse section area
Ships
For ships, an elaborate method (e.g., Holtrop-Mennen method) to calculate calm water resistance is usually recommended to get more accurate current force.
Wave forces
The current force calculated above is actually the force which the vessel will experience in calm water. However, the sea is a dynamic environment because of waves which the vessel encounters. These waves add to the forces on the vessel and are these forces are called as ‘Added Wave Resistance’ or the ‘wave drift force’.
Wave drift force depends on the dimensions of the vessel, and its shape. The method for calculation of added wave resistance is provided in DNV-RP-H103 Modelling and Analysis of Marine Operations Sec 7.2.6 (see below extract).

Source: DNV-RP-H103 Modelling and Analysis of Marine Operations
Towing Efficiency
How do we get towing efficiency?
The tug’s efficiency is affected by many factors, like, size of tug, the harshness of environment, and the towing speed. ND-0030 provides a table to calculate the towing efficiency of the Tug. If the tug’s Continuous Bollard Pull is BP, then the table provides following values for the Towing efficiency
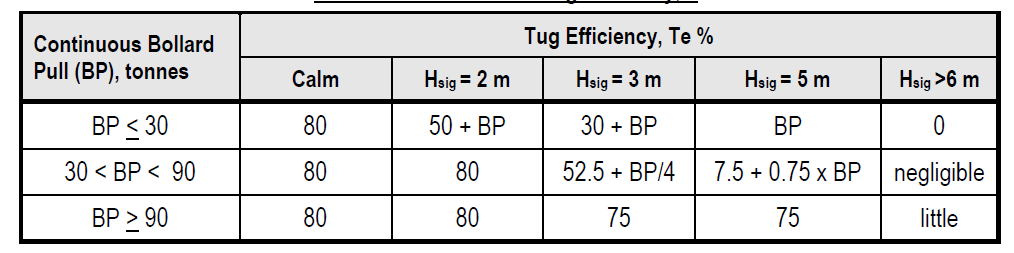
Source: ND-0030 Guidelines for Marine Transportations
Calculation of Required Bollard Pull
Now that we have the wind, wave and current forces, we can calculate the total resistance force on the vessel as
FTOT = FWIND + FWAVE + FCURRENT
Then the required Bollard Pull can be calculated as
Required BP = FTOT/ƞ
The continuous bollard pull of tug must be higher than the Required BP for the tug to be suitable for towing.
SECTION E – The role of Marine Warranty Surveyor (MWS)
The Marine Warranty Surveyor has a very critical role in towing operations. His role includes, but is not limited to
- Survey of vessel and tug for towing equipment and general condition
- Approval and acceptance of environmental conditions/weather data
- Review of the bollard pull calculations
- Witness and review of Bollard Pull tests, if required to be performed
- Review and approval of the towing plan
The towing operator has to work closely with the MWS by providing all documents and calculations on time and getting MWS approvals prior to the operation. The potential areas of contention with the MWS might be the following, and the towing operator should carefully prepare the supporting documents to get MWS approval in time
- Disagreement over environmental criteria adopted
- Non-willingness of MWS to grant benign weather criteria
- Disagreement over the method adopted for Bollard Pull calculation
- Disagreement over the condition of the tug
- Insistence to carry out a Bollard Pull test to confirm the rating of the tug
While the above are not regular occurrences, it is advisable for the towing operator to be proactive in treading these issues to avoid delays and surprises during the operation.
That leads to the conclusion of this Part – I. In Part – II we will discuss the method of calculating the maximum feasible towing speed for a given environment.
References
- DNV RP-H103 Modelling and Analysis of Marine Operations
- ABS, 2016, Rules for Building and Classing Mobile Offshore Drilling Units, Part 3 Chapter 1,Section 3, ‘Environmental Loadings’, p.11.
- An Approximate Power Prediction Method, J.Holtrop and G.G.J.Mennen, 1982
- BV – Towage at Sea of Vessels or Floating Units
- OTC 3220, Vol 4, Resistance of Offshore Barges and Required Tug Horsepower
Disclaimer: This post is not meant to be an authoritative writing on the topic presented. thenavalarch bears no responsibility for the accuracy of this article, or for any incidents/losses arising due to the use of the information in this article in any operation. It is recommended to seek professional advice before executing any activity which draws on information mentioned in this post. All the figures, drawings and pictures are property of thenavalarch except where indicated, and may not be copied or distributed without permission.
PS: TheNavalArch has its own products for calculating Bollard Pull required for Barges and Ships. Check them out below.
[/cmsms_text][cmsms_text animation_delay=”0″]


It’s a useful explanation for non-naval people.Am working in offshore rig;i had doubts about BP of AHTV.Now fully understood.Thanks.
Hi Subash
Happy to know it helped you. Hope to serve you with better articles in future.
Prem Shankar
Greetings,
Kindly provide in direct towing calculation against tug and tanker ship escorting assisting operations for berth / unberth single buoy mooring loading terminal.
Best regards,
Steve
Thank You
This is helpful. We’re a charity that is involved in relief. We’re considering a 350 HP tug for handling FlexiFloats.
I just started reading your information. I hope there is a section on Kort nozzels.
Hi Joe
Happy to know this. Should you need any engineering help with any of your projects, you’re welcome to get in touch info@thenavalarch.com. Thanks again, and please do keep visiting.
Just wanted to know what the calculation was for Bollard pull to Horsepower and vice versa.
Hi Kenneth
Thanks for your query. A thumb-rule is one ton pull per 100 horsepower for a conventional propeller, or 1.2 to 1.5 tons pull per 100 horsepower for a propeller fitted with a nozzle
http://www.imcbrokers.com/blog/overview/detail/bollard-pull
I’m interested of a bollard pull calculation for a tugboat, based on shape of the vessel, main engines capacity and type of proppellers. There is a chance to help me with it?
Hi Gelu
Thanks for your query. We have dropped you an email. Will follow up from there.
Could you possibly assit me with a rule of thumb for a push aspect.
Hi Erik
Thanks for your query. The same principles will apply, whether it is a pull or a push – calculate the forces and get the required bollard pull = Force/efficiency. Rules of thumb are not recommended for a reliable result. Hope this helps!
Hello,
We operate in a largely unregulated and non-standard market and most of the tug boats are locally made. I have a situation where we requested a 1500HP boat as a lead tug to tow a swamp barge and we ended up losing the barge to water current as the boats could not hold against the current. The barge sustained considerable damage as a result of collision with the river bank.
Presently, we don’t have a setup to test these tugs for the real bollard pull figures. I have watched a few bollard test videos on utube and wondering if it is something we can set up to qualify boats whenever we require their services.
Hi Nnamdi
Thanks for the query, and apologies for the delay in response.
The most certain method to establish a tug’s pulling power is a bollard pull test. While our calculator can help you in knowing how much bollard pull will be required to tug a particular vessel, it won’t help you establish the pulling power of a tug. Especially for older tugs, it is strongly recommended to conduct a test to establish their real BP compared to what’s on paper.
Hope that helps. Let us know if you have more questions. You can also email us at info@thenavalarch.com
Aren’t wind speeds given at 10m reference heights? So, technically you should be able to use a lower wind speed at cargo heights below 10m. amirite?
WHAT WILL BE TH BOLLAR PULL FOR A TANKER HAS FOLL SPECIFICATION
-Loa 349
-l.p.b 331
-breadth moulded 52
-depth moulded 25.5
-max dwt 253,450 mt
-max draft 20.-12
-min draft 10 m
-crude oil storage capacity min: 238,480 cu
-crude oil storage capacity:1,588,411 bbls
-max receiving rate:23,848 cu
-max export rate:10,000 cu
Wanna read
I have two questions when I use your Exel Sheet by thenavalarch for bollard pull calculation.
1. Why the efficiency is used as 0.75?
2. When 2 tug boat is used for a vessel, the bollard pull of one tug boat is the half of the calculated bollard pull?
or we have to have more margin than calculated for a vessel?
Your explanation would be very helpful if we predict the proper Bollard pull for one tugboat when we use two tug boats at the same time.
Hi Sik Lee
We already had discussions over email to sort this out. Thanks for your support
Hi Sirs,
It was used a speed of 20 m/s instead of 40 knots for the wind forces presented on table at Step 5. Therefore, the wind forces values shall be less than the presented on the table.
Kind Regards,
WHAT IS BOLLARD PULL FOR TUG MUST TOW BARGE DWT 1500