Description
What does this App do?
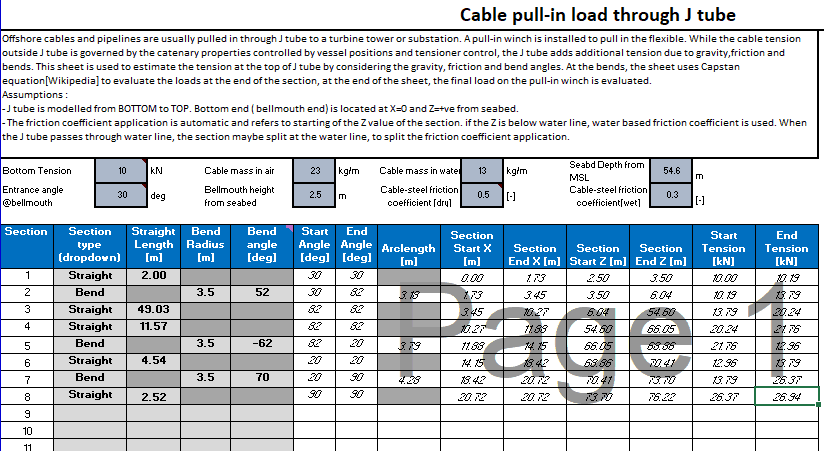
Offshore cables and pipelines are usually pulled in through J tube to a turbine tower or substation. A pull-in winch is installed to pull in the flexible. While the cable tension outside J tube is governed by the catenary properties controlled by vessel positions and tensioner control, the J tube adds additional tension due to gravity,friction and bends. This sheet is used to estimate the tension at the top of J tube by considering the gravity, friction and bend angles. At the bends, the sheet uses Capstan equation[Eytelwein’s formula] to evaluate the loads at the end of the section, at the end of the sheet, the final load on the pull-in winch is evaluated.
How to use this app?
User can add straight sections or bends with their properties
Upto 20 sections can be added
The properties of each section or bend are evaluated, and the cumulative property is also calculated
The input cells are all in blue. All parameters are in SI units
Limitations
“- J tube is modelled from BOTTOM to TOP. Bottom end ( bellmouth end) is located at X=0 and Z=+ve from seabed.
– The friction coefficient application is automatic and refers to starting of the Z value of the section. if the Z is below water line, water based friction coefficient is used. When the J tube passes through water line, the section maybe split at the water line, to split the friction coefficient application. ”
References
The app is based on the Eytelwein’s formula (or Capstan equation)
![]()
Tload is the applied tension on the line
Thold is the resulting force exerted at the other side of the capstan
μ is the coefficient of friction between the rope and capstan materials
ϕ is the total angle swept by all turns of the rope, measured in radians
“Several assumptions must be true for the formula to be valid:
1. The rope is on the verge of full sliding, i.e. Tload is the maximum load that one can hold. Smaller loads can be held as well, resulting in a smaller effective contact angle ϕ .
2. It is important that the line is not rigid, in which case significant force would be lost in the bending of the line tightly around the cylinder. (The equation must be modified for this case.) For instance a Bowden cable is to some extent rigid and doesn’t obey the principles of the Capstan equation.
3. The line is non-elastic.”
Revision History
20-Nov First Issue






ROBERTO CHAVEZ (verified owner) –
the calculator is a good tools that helps to get quickly results in J tube tension calculations; however, I do not undesrtood why in the preloaded example is indicated a negative angle that reduce the tension. I believe that all angles shuld be positive because Capstan formulation does not refer to use positive or negarive angles.
Please explain why is considered a negative angle for this calculation.
Best regards
Roberto