Barges are the simplest, and yet most widely used of marine vehicles. They are used for a variety of purposes ranging from carrying cargo in bulk or liquid, to even carrying passengers for short inland cruises. Barges are mostly towed by another barge called a tug, but some barges can also be self-propelled. Barges are also mostly used on inland waterway routes and lakes/rivers, but many offshore barges are used for long-distance open-ocean transportation also.
Barges are flat-bottomed, and box-shaped, which makes their design and construction quite simplified.
Knowing the trim and stability of a Barge during operation is an important input to successful operation/voyage of the Barge. Stability would mean that the barge should have sufficient righting moment to bring it back to an upright position in case of heeling.
IMO Criteria for Stability
The International Maritime Organization (IMO) is the international statutory authority which has laid out the criteria for Stability to be met by all barges, including Barges. These are contained in its document ‘IMO 2008 Intact Stability (IS) Code’. Basically, the Stability criteria are parameters which are calculated on the righting arm curve of the barge (also called the GZ Curve), and IMO requires these parameters to meet certain minimum requirements. The IS Code lays out the stability criteria for all types of barges, and it also provides specific criteria applicable to non-self-propelled Barges (or pontoons) carrying deck cargo.
In this article, we’ll explore the Stability requirements Barges, including that of a special type of Barge which is non-self-propelled and carries deck cargo. Such Barges are called ‘Pontoons’.
How to decide which criteria to apply?
To decide which criteria to apply, it is important to know the type of Barge. If it is a pontoon, as defined in Part B, Ch2, Sec 2.2.1 of IS Code 2008, then the pontoon stability criteria apply. The definition of a Pontoon is shown in the picture below:
Definition of Pontoon [2]
The Stability criteria to be met by the GZ curve of a pontoon are in Sec 2.2.4 shown below:
Pontoon Stability Criteria [2]
If the barge doesn’t satisfy the definition of Pontoon as above, then the general Stability criteria as in Part A, Ch 2, Sec 2.2 of IS Code 2008 shall apply. The general criteria are shown below:
General Stability Criteria applicable to all vessels [2]
Further, if the Barge is meant for some specialized operation (e.g., Crane Barge or Jack-up barge), then special criteria applicable to these types of barges will apply. In this article we will limit ourselves to deck cargo barges and pontoons.
Stability Calculation for an existing Barge
If you have an existing barge for which the following documents are available, then the Stability calculation can be done using an excel-based interface, some formula and programming using the VBA developer interface of Excel.
Documents required
- Hydrostatic particulars and cross curve data of the barge
- Capacity Plan – showing the geometry of tanks and their capacity
- Tank Tables – showing filling of tanks at different levels
- General Arrangement
- Location of downflooding points (Read about downflooding points here)
Methodology
Now we will talk a bit about the methodology behind the computation, by using a reverse thinking process.
The objective of the whole exercise if to find out the following:
- The trim and hydrostatics of the floating condition
- Stability – righting arm curve
Trim and Hydrostatics of Floating Condition
The trim and hydrostats at a floating condition is dictated by the total weight and the position of the Center of Gravity at that floating condition. The total weight will comprise the self-weight of the barge (lightweight), the weight of provisions, crew (if any), the weight in tanks, and deck cargo (if any). All these inputs can be taken from the user in a tabular format. Next, we need to get the trim/hydrostatics of the floating condition. For this, let’s understand what hydrostatics mean – the hydrostatic properties of the floating condition are those properties which change with a change in the loading. For example, the draft of the barge changes with changing loading and is a hydrostatic property. Similarly, the center of buoyancy of the barge changes with the changing loading, and so it is another hydrostatic property. Here we list down the common hydrostatic properties that are used to assess a floating condition:
| Final Hydrostats | |
| Displacement | Determined by the total weight of the barge |
| Mean Draft | The level at which the barge floats |
| LCB | The longitudinal center of buoyancy |
| VCB | The vertical center of buoyancy |
| TPcm | The Tons Per cm of immersion – weight required to immerse the barge by 1 m |
| LCF | The longitudinal center of floatation |
| MCTcm | Moment to change trim by 1 cm |
| KMl | The metacentric radius (longitudinal) |
| KMt | The metacentric radius (transverse) |
| Total Trim | The difference between drafts of aft and fwd ends |
| KG | The vertical center of gravity |
| FSM Correction | Free Surface Moment in tanks (leads to correction in KG) |
| KG(corrected) | Vertical center of gravity corrected for FSM |
| GM(transverse) | The metacentric height (KM-KGcorrected) – transverse |
| GM(long) | The metacentric height (KM-KGcorrected) – longitudinal |
| Heel | The heel of the barge in equilibrium position |
The above parameters are unique to a specific loading condition of a barge. How can hydrostatics be calculated? The steps are listed below:
- Calculate the total weight (W) of the barge in the floating condition – this includes lightweight plus deadweight (weight in tanks + weight of crew/provisions + deck cargo)
- Calculate the vertical center of gravity of the barge (KG) measured from the keel (or any other reference point) in the floating condition
- Check the hydrostatic table of the barge, and find out the two rows whose displacement values are just higher than and just less than W.
- Interpolate between the two rows to find out the value of draft, KM, LCB, VCB, TPcm, MCTcm
- Calculate the FSM effect from the level of filling in tanks, and from the standard formula for FSM
FSM effect for a tank = (Tank density/Sea Water Density) x (Transverse Moment of Inertia of a tank/Barge’s Displacement)
FSM effect for all tanks is them summed up to give the net effect on the KG of the barge (it raises KG). The corrected KG is given by KGcorrected = KG + FSM effect
- The metacentric height (GM) can be calculated from the formula
GM = KM – KGcorrected
- Heel: equilibrium Heel can be obtained by calculating the transverse Center of Gravity of the barge in the loading condition. From the transverse Center of Gravity, the transverse heeling moment on the barge can be calculated. The heeling moment curve can be superimposed on the righting arm curve to give the heel as their intersection point.
The righting arm curve and Stability
Once hydrostats have been calculated, the next exercise aims at finding the righting arm curve of the barge for a given loading condition, with a specific configuration of tanks. Basically, the righting arm curve is calculated from a formula as below:
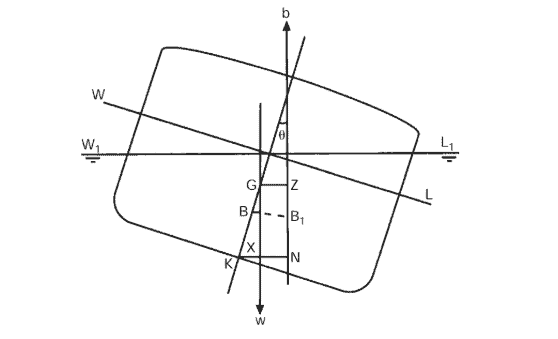
GZ = KN – KG sinθ
Here, GZ = righting arm, KN = the lever arm obtained from cross curves (also called KN curves). KG is the vertical center of gravity of the barge in the loading condition, measured from a reference point K (K is generally taken as the baseline of the barge). The whole concept is shown in the figure below:
GZ calculation from KN [3]
Thus, the three parameters which are needed for getting the GZ curve are:
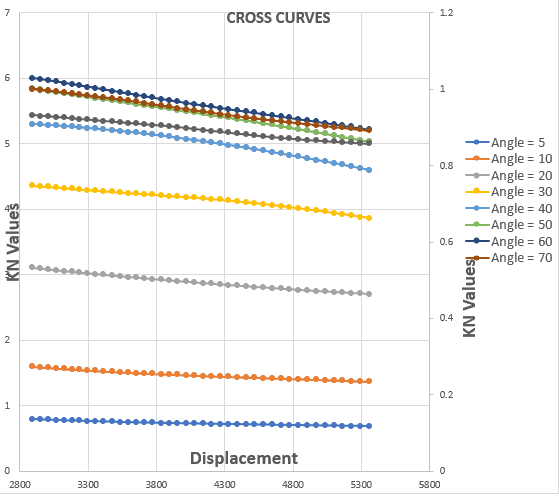
- Cross curve, KN. These can be obtained from the cross-curve table of the barge which is generally available in the stability booklet of the barge. These are plotted vs the displacement of the barge, and for different angles of heel, and look like below:
Stability Cross Curves
- The vertical center of gravity (KG) above the baseline – this is calculated from the total loading of the barge – including its lightweight, tank weights, weight of provisions/crew and deck cargo weight (if any)
- The angle of heel (θ)
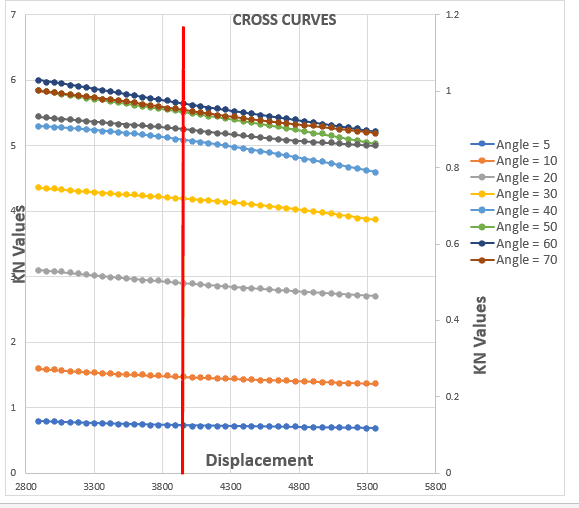
To plot the GZ curve for a given loading condition, we will need to know the KN values for different angles of heel for that loading condition. For doing this, we calculate the displacement of the loading condition and use the cross curves chart/table to get the KN values. We can see it demonstrated from the graph below
Getting KN values at displacement 4000 MT
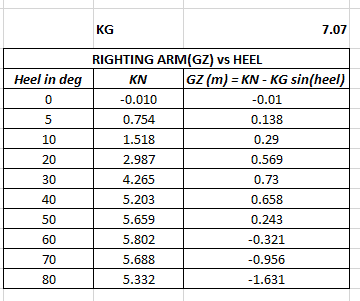
Once we have the values of KG, and KN for different angles of heel, we can calculate the values of GZ for different heel angles in a tabular form to generate the GZ curve
GZ calculation from KN
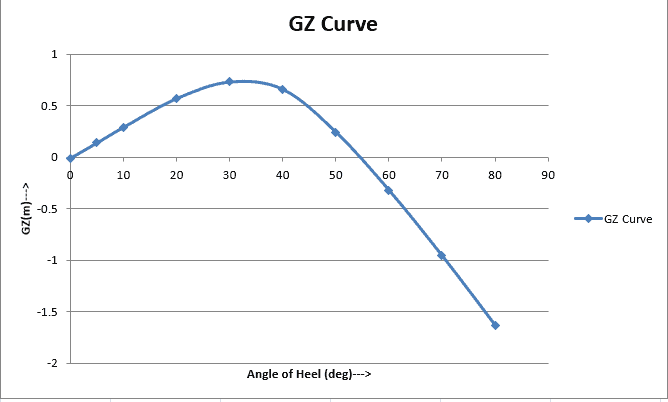
The resulting GZ curve will look like the below:
Righting Arm (GZ) Curve vs Heel
Evaluating Stability parameters as per IMO A.749(18)
Next, we need to calculate how the GZ curve fares on the Stability parameters.
Case 1: for Barges which are not Pontoons
For these Barges, the IMO general criteria will apply
| Sl.No. | Parameter | Method of calculation |
|
1 |
The area under the righting lever curve (GZ curve) should not be less than 0.055 metre-radians up to 30° angle of heel.
|
By numerical integration of the GZ curve |
|
2
|
The area under the righting lever curve (GZ curve) should not be less than 0.09 metreradians up to 40° angle of heel or the angle of downflooding if this is less than 40°.
|
By numerical integration of the GZ curve |
|
3 |
The area under the righting curve between the angles of heel of 30° and 40° or between 30° and the angle of downflooding if this angle is less than 40°, should not be less than 0.03 metre-radians. | By a difference of areas in Criteria 1 & 2 |
|
4 |
The righting lever GZ should be at least 0.20 m at an angle of heel equal to or greater than 30°. | Directly from the GZ curve, by measuring the value at 30 degrees |
|
5 |
The maximum righting arm should occur at an angle of heel preferably exceeding 30° but not less than 25°.
|
By finding the maximum of the GZ curve |
| 6 | The initial metacentric height GMo should not be less than 0.15 m. | From hydrostats table |
Case 2: for Barges which are Pontoons
For these Barges, the specific Pontoon Criteria will apply
| Sl.No. | Parameter | Method of calculation |
|
1 |
The area under the righting lever curve (GZ curve) upto maximum GZ should not be less than 0.08 m-rad
|
By numerical integration of the GZ curve |
|
2
|
The static angle of heel due to a wind of speed 30 m/s should not exceed an angle corresponding to half freeboard
|
By calculating the angle of heel by superimposing wind heeling moment on GZ curve, and calculating the freeboard from the hydrostats |
|
3 |
Minimum range of Stability should be 20 degrees for Length of pontoon <= 100 m, and 15 degrees for Length of pontoon >= 150 m, and by interpolation in between | By calculating the angle of heel at which GZ becomes zero (other than the equilibrium angle) |
IMO Weather Criteria
Similar to the standard stability criteria listed above, there’s also IMO Weather criteria for barges. These are applicable for barges which are not pontoons, and for which the general IMO Stability Criteria apply. These are shown below:
IMO Weather Criteria
For calculating the IMO weather criteria, we need to calculate the heeling moment which a barge experience due to a wind from transverse direction. The heeling moment is divided by the displacement of the barge in the loading condition to give the heeling arm. This heeling arm is plotted on the GZ curve to evaluate the stability parameters for the weather criteria. This is shown in the figure below:
GZ Curve for Weather Criteria
The whole process can be put into multiple steps:
- Get the user to input vessel’s basic geometry, lightweight, hydrostatics and cross curve data in tables
- Get the user to input tank geometry (tank tables)
- Get other information like downflooding points in tabular format
- Prepare a spreadsheet for a typical loading condition in which the user can change the tank filling, and add any deck cargo
- Evaluate the hydrostats of the loading condition
- Use the hydrostats to get KN values for the loading condition
- Generate the GZ curve using KN values
- Calculate the Stability parameters from the GZ curve
The steps 1 to 8 above can be put in the form of an MS Excel workbook with a separate worksheet for each step. With some excel VBA programming in the background, the workbook can be used to create a custom Stability calculator for a vessel and can be used to determine the loading and stability of the vessel every time a new voyage/operation is to be undertaken.
That brings us to the end of this article. If the data of an existing barge is available, then the Hydrostatics and Stability of the barge can be evaluated by following the basic formulations of Stability.
Please do take some time to explore TheNavalArch’s Stability Suite: three products that are used for three different barge types.
- ShipStab – is for all cargo barges which are covered under the IMO general criteria in Part A, Ch 2, Sec 2.2 of IS Code 2008
- PassStab – is for Passenger barges, which have additional criteria in Part A, Ch 3, Sec 3.1 of IS Code 2008
- PontoonStab – is for all pontoons which are covered in Part B, Ch 2, Sec 2.2 of IS Code 2008. Due to be launched on 9th July, 2020
References:
[1] Principles of Naval Architecture, Edward V. Louis, Ch II
[2] IMO Res A.749(18)
[3] Barge Stability for Masters and Mates, By Bryan Barrass, Capt D R Derrett
Disclaimer: This post is not meant to be authoritative writing on the topic presented. thenavalarch bears no responsibility for the accuracy of this article, or for any incidents/losses arising due to the use of the information in this article in any operation. It is recommended to seek professional advice before executing any activity which draws on information mentioned in this post. All the figures, drawings, and pictures are property of thenavalarch except where indicated, and may not be copied or distributed without permission.
TheNavalArch Interview Series: Mr. Balakrishna Menon
Mr. Balakrishna MenonEngineering Director Mooreast (Asia) Pte Ltd TheNavalArch's Interview Series is an endeavor to get insights from the best engineering and business brains in the industry, and present them to its users for the larger...

Floating Rice Fields, the quest for solutions to combat drought floods and rising sea levels
by Lim Soon Heng, BE, PE, FSSS, FIMarEST Founder President, Society of FLOATING SOLUTIONS (Singapore) Abstract Amazing as it seems, there is a case for growing rice on floating platforms in the sea. The capital expenditure to develop this is offset by the opportunity...

CAPSIZE OF LIFTBOAT IN TRANSIT
This paper was originally presented in the 27th Offshore Symposium, February 22nd, 2022, Houston, Texas Texas Section of the Society of Naval Architects and Marine Engineers It has been reproduced here for the readers of TheNavalarch INTRODUCTION In 1989 a Class 105...

Designing a closed chock as per IACS rules
Introduction Chocks are used universally for mooring and towing operations on ships. For towing operations, Chocks are used for guiding the towing rope from the winch through the outer shell of the vessel to the tug. For mooring operations, the chock is used to...
The Optim22 method of hull optimization – Part 2
This is a follow-up article to the previous article on Framed Structures Optimization. 1.1 Abstract A previous article introduced the Optim22 method. This one adds additional background information plus 3 more case studies to...

The Optim22 Method of Weight Optimization of Framed Steel Structures
1 Abstract A semi-automated structural weight optimization system is presented for framed structures of post and beam construction which is based on basic structural member design principles. The approach is to adjust member properties in a manner that...

Combating rising seas with floating structures
Introduction Rising sea level is an existential threat for many coastal cities. The sea is rising subtly but relentlessly at an exponential rate. Many predictions of how high and how fast it will rise in the next 50 years have proved to be understated. According to...

Sea Pressure Loads Calculation based on DNV Rules
Introduction Sea pressure loads are an important factor in the structural design of a vessel. What is sea pressure load? As the term suggests, it is the external pressure on the vessel due to the surrounding sea. What kind of pressure it is, and how to...

A quick empirical method for resistance estimation of planing vessels
Resistance estimation for a vessel is a fundamental exercise in design of the vessel. Resistance is a property that depends on the vessel’s shape and form. A conventional ship-shaped vessel with a bulb will have completely different resistance characteristics compared...

Powering the maritime industry with Hydrogen – Part 2
Powering the shipping industry with hydrogen - Part 2: Hydrogen propulsion on a ship - opportunities and challenges Introduction In the Part 1 of this article, we explored the basic properties of Hydrogen as a fuel, and also the opportunities and challenges...







I’m an independent Marine Surveyor interested to find information about the Barge’s stability.
Hi Virgilio
Thanks for your interest. You’re welcome to write to us at info@thenavalarch.com
I am a marine manager, interested to create a stability calculation spreadsheet for our small company in Papus New Guinea.
Please check your email
Hi
I have a case where I need to calculate the stability for a barge, could I get a copy of your excel sheet?
Hi Eric
Thanks for your query. At the moment it is not available for trial. You can watch the video to see how the software works. If you have any questions please send to info@thenavalarch.com
Hi, could I get a copy of your excel sheet please?
Hi
Thanks for your query. At the moment it is not available for trial. You can watch the video to see how the software works. If you have any questions please send to info@thenavalarch.com
Hi, could I also get a copy of your excel sheet please? Thanks in advance.
Hi
Thanks for your query. At the moment it is not available for trial. You can watch the video to see how the software works. If you have any questions please send to info@thenavalarch.com
Hi,
May I request to have a copy of the excel sheet please? Currently working on barge and pontoons and would be good to have this kind of reference just to start with. Many thanks.
Hi Mac
Thanks for your query. At the moment it is not available for trial. You can watch the video to see how the software works. If you have any questions please send to info@thenavalarch.com
Hi ,
I’m work for small transport company in VietNam, some time transport cargo by pontoon.
Could I also get the copy of your excel sheet please ?
Hi Ahmed
Thanks for your query. At the moment it is not available for trial. You can watch the video to see how the software works. If you have any questions please send to info@thenavalarch.com
Hi Minh
Thanks for your query. At the moment it is not available for trial. You can watch the video to see how the software works. If you have any questions please send to info@thenavalarch.com
Hello
Could I also get the copy of your excel sheet please ?
Im working in a building company, and from time to time we need to transport your equipment and materials on barge.
Best regards.
Hi Ahmed
Thanks for your query. At the moment it is not available for trial. You can watch the video to see how the software works. If you have any questions please send to info@thenavalarch.com