This is a follow-up article to the previous article on Framed Structures Optimization.
1.1 Abstract
A previous article introduced the Optim22 method. This one adds additional background information plus 3 more case studies to illustrate its application. The choice of optimization input parameters is the subject of ongoing study.
1.2 Introduction
An automated system (referred to herein as the Optim22 method) to assess structural weight-optimization of modules of standard post-and-beam construction ie built up mostly of structural members was introduced in a previous article. Recall that possible applications for it are:
- Assessment of structural analysis models provided to facility owners by 3rd Party design consultants with regard to modeled structure weight
- Generation of more reliable Concept and FEED primary structure estimates than generally available using weight norms that are often based on limited data.
Re: point 2, the method permits rapid evaluation of multiple structural configurations. For both applications, the product is an optimized structural analysis model that can be independently verified.
In a nutshell, the Optim22 method employs basic member design principles and iteratively adjusts member section properties of a structural analysis model in a controlled manner. A structural model of a given configuration is “unity-check” optimized to section-specific target unity check values at each iteration. By implication, this is expected to lead to weight-optimized designs for given structural configurations.
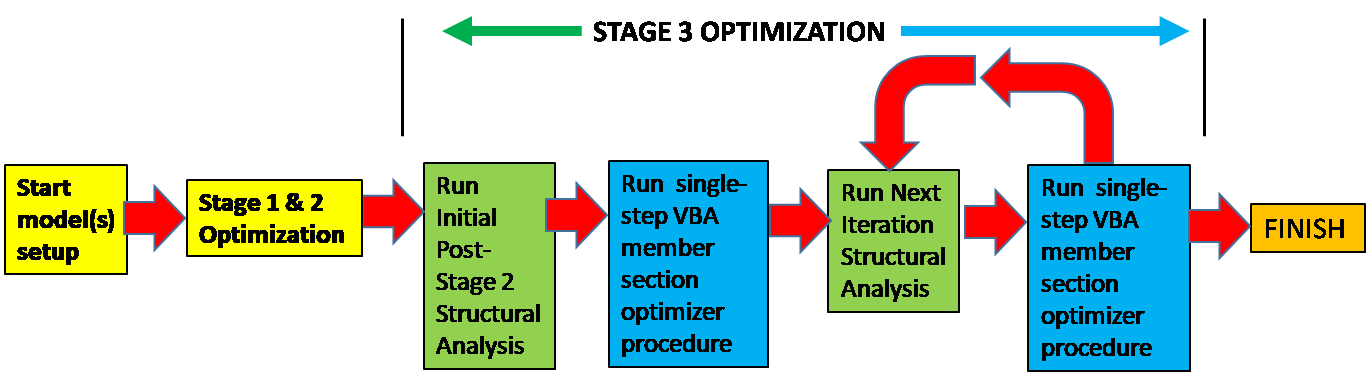
The procedure is summarized in Figure 1 which is reproduced from the previous article.
Figure 1- Structural Analysis Models Optimization Procedure
The remainder of this article presents further details of Stage 3 Optimization illustrated with case studies based on a recent project.
1.3 Setup Considerations
The Optim22 method has been set up to accommodate structural analysis models produced by a range of engineering organizations so that a wide variety of modeling conventions are expected. This can present a challenge when dealing with models created by 3rd Parties as there is a wide range of valid modeling conventions. To handle this, the form of structural models is “standardized” to allow them to be processed with a common analysis workflow. This simplifies the handling and updating of the analysis inputs between Optim22 Stage 3 iterations.
Referring to Figure 1, no further setup is required once the model of interest is converted to the standardized form but the number of iterations required at Optimization Stage 3 is generally decreased if the model is subject to Stage 1 and/or Stage 2 optimization. Refer to the previous article for further description of the three stages illustrated in Figure 1.
1.4 Nomenclature
Nomenclature and definitions introduced in the previous article are repeated here for convenience.
Table 1- Definitions and Nomenclature
| Term | Meaning | Term | Meaning |
| Grup | Set of modeled members with common material and section properties (Note: “Grup” is SACS program terminology.) | ALARP | As low as reasonably practical |
| UC | Unity Check value/ratio (nominally a calculated value divided by an allowable value) | ||
| UC_Tot | Total Unity Check | UC_SoC | Sum of component UC’s (see Article 1, eq. 2) |
| UC_ax | Axial (tension/compression) component of total unity check value | UC_ax-M | Maximum UC_ax overall members in a “grup” |
| UC_yBend | Member local y-axis bending component of total unity check value | UC_yBend-M | Maximum UC_yBend overall members in a “grup” |
| UC_zBend | Member local z-axis bending component of total unity check value | UC_zBend-M | Maximum UC_zBend overall members in a “grup” |
| Ax, | Member cross section area | CoG | Center-of-gravity |
| SMy | Member Section Modulus with respect to local y-axis bending (generally strong axis of I-shapes) | ||
| SMz | Member Section Modulus with respect to local z-axis bending (generally weak axis of I-shapes) | ||
1.5 Optimization Stage 3 Methodology Details
Again reference is made to Figure 1 presented in the introduction to this article. Further details on the selections of the various optimization parameters utilized in Optimization Stage 3 are presented here. (Refer to the previous article for a description of Optim22 Stages 1 & 2.)
Selection of Unity Check (UC) increments at each step of optimization is the key to the whole procedure. It is noted that these are not cast in stone at the present time since Team NavalArch expects to continue to uncover additional considerations to be accounted for as new structural analysis models are subjected to the Optim22 procedure.
In the previous article, the relationship
UC_Tot,i = UC_ax,i + UC_yBend,i + UC_zBend,i {eq 1}
was introduced where “i” pertains to the i-th iteration of the Optim22 Stage 3 procedure. Note that eq 1 applies strictly to individual members but in the Optim22 procedure it is applied to “Member Grups” with UC,ax AND UC,yBend AND UC,zBend being the “envelope” maxima for a Grup. It is noted that if all members in a Grup were loaded exactly the same, all members in a Grup would exhibit the same UC value so the Grup maximum UC would apply to all members. Of course, this is not likely to occur in practice. (Optim22 Stages 1 and 2 are attempts to arrive at an assignment of member Grups where all constituents have more similar loading.)
For the next Stage 3 analysis iteration ie the (i+1)th iteration , the properties of the active members are adjusted on a Grup-By-Grup basis via the following three-step method:
STEP 1: Establish incremental UCax and UCbnd changes (ie dUCax, dUCbnd) to apply to ith iteration results to obtain targets for (i+1)th iteration
- Set Global Guiding Parameters (defined by User)
| UC,SoC,targ | Global target value for the Sum of Member Unity Check components (ie axial and bending about two orthogonal axes | |
| f_incr | UCax target lower bound | |
| f_UC(SoC-max) | Factor to be applied to the spread between Ucmax,i and UC,SoC,i | |
| UC,SoC,GrpModif | GRUP specific Factor applied to UC,SoC,I ( 0<UC,SoC,GrpModif<1) |
- Calculate Iterative Guiding Parameters (developed utilizing current analysis results)
| UCax,i AND UCax,i+1 | Grup Max Unity Check (Axial) for the ith and (i+1)th iterations respectively | |
| Uceul,i | Grup Max Unity Check (Euler Buckling) for the ith iteration | |
| UCyBnd,i AND UCyBnd,i+1 | Grup Max Unity Check (y-Bending) for the ith and (i+1)th iterations respectively | |
| UCzBnd,i AND UCzBnd,i+1 | Grup Max Unity Check (z-Bending) for the ith and (i+1)th iterations respectively | |
| UCmax,i | Max Unity Check over all members in the Grup for the ith iteration | |
| UC,SoC,i | Sum of Max Component Unity Checks (UCax,i + UCyBnd,i + UCzBnd,i) for the ith iteration | |
| Alfa,i+1 | Factor equal to UCtarg,i / UC,SoC,i |
- For each GRUP being optimized, calculate
| f_1 = Alfa,i+1 = UCtarg,i / UC,SoC,i | |
| f_2 = n2 where n2 is an integer selected based on test trials (eg n2= 5, 2, 1 etc) | |
| f_3 = n3 where n3 is an integer selected based on test trials (eg n3= 5, 10 etc) |
- Determine UC increment estimates as follows:
| dUCax,i = (UCmax/UC,SoC) *(f_1 -1) *(UCax,i / f_2)
(if Max(UCax,i, UCeul,i) > f_incr) |
dUCyBnd,i = (UCmax/UC,SoC) *(f_1 -1) *(UCyBnd,i / f_2) | dUCzBnd,i = (UCmax/UC,SoC) *(f_1 -1) *(UCzBnd,i / f_2) |
| = Max(UCax,i, UCeul,i) / f_3 (if Max(UCax,i, UCeul,i) < f_incr) |
- Finally, determine targets for the next step UC components:
| UCax,i+1 = UCax,i + kDlt * dUCax,I | UCyBnd,i+1 = UCyBnd,I + dUCyBnd,i | UCzBnd,i+1 = UCzBnd,I + dUCzBnd,i |
| where kDlt = +1 if UCmax < UC,SoC_target | ||
| = -1 if UCmax > UC,SoC_target | ||
STEP 2: Determine the target Section Properties to be assigned to the Grups being adjusted in the next analysis iteration
| Ax is inversely proportional to UCax so let Ax,i = C1\UCax,i | ||
| SM is inversely proportional to UCbnd so let Smy,i = C2/UCyBnd,i and SMz,i = C3/UCzBnd,i | ||
| Can calculate C1, C2 & C3 for the “current” analysis results ie the i-th iteration | ||
| Set next iteration section property target values based on these C1, C2 & C3 ie | ||
| Ax,i+1 = C1/UCax,i+1 | SMy,i+1 = c2/UCyBnd,i+1 | SMz,i+1 = c3/UCzBnd,i+1 |
STEP 3: From (pre-generated) member property tables, find candidate member cross sections Ax,Cand and SMy,Cand and SMz,Cand such that all THREE of the following relationships are satisfied:
| 1 | 2 | 3 | |
| Ax,Cand => Ax,i+1 | SMy,Cand => SMy,i+1 | SMz,Cand => SMz,i+1 | where “=>” means greater than or equal to |
Finally, select the “candidate” with the smallest area ie the “lightest” one.
It is noted that section modulus (SM) tends to be the dominant parameter for beam/girder design while cross section area (Ax) tends to be most significant for Column & Brace design but ALL three of Ax, SMy, and SMz need to be considered in the selection of the targets.
1.6 Case Studies based on Recent Project
1.6.1 Overview
Recall that two case studies were reported in the previous article to illustrate the Optim22 optimization process. These were based on projects executed in the 2014-2018 period. In this article, an additional three case studies based on a recent FPSO topsides project are presented to illustrate the application of the Optim22 Stage 3 method to structural models with a range of support conditions and stages of design development.
As in the previous case studies, the structural analyses in all cases are performed using the SACS software where further analysis automation has been made available to the SACS Users that was not available previously. In the standard analysis workflow followed, design conditions considered are Lift, FPSO transit, one-year operating, 100-year storm, and FPSO static heel and trim in a damage condition. (Hog and sag deflection effects are considered in addition for modules with multi-point support systems.) The structural loading derives primarily from “weight” i.e. gravity and inertia due to FPSO motions although wind load is also considered. Fatigue of welded-connections is not considered. In all analyses, module weight is invariant at each optimization iteration except for the modelled structure since it is subjected to the optimization process presented above.
The main purpose of this article is to further illustrate Stage 3 of the Optim22 process so Stages 1 and 2 are not carried out for the Case Studies presented here though it will be seen that they could have benefited from it. The main benefit of executing both Stage 1 and Stage 2 is that it can lead to a set of member Grups with less variation in loading across constituent members.
Overall member unity check plots where the governing UC values over all design conditions, both Lift and In-situ conditions are presented on a single plot. A common contour scale is employed ie
Same as in the previous article, the effectiveness of the optimization strategy is demonstrated by Before-Vs-After member “Grup” maximum unity check value comparisons. For all case studies, the target “Total” member UC value was set as 1.0.
In addition, the variation of modeled weight of structure at each iteration is tracked.
1.6.2 CO2 Compression Module at Detail Design Status
This model is based on a relatively mature structural design of a module on a recent FPSO delivery project, referred to as MP3 here. It was developed by a 3rd Party and adapted here for processing via the standardized analysis workflow employed in the Optim22 method.
Figure 2- SACS model for CO2 Compression Module
This model is shown above in Figure 2 and the total “pre-optimized” dry and operating weight considered was 1250/1400 MT. It features two main deck levels with a service platform on the upper level. The support system is a “multi-point” system of rigid and flexible stools in a 5×3 (rows) stool arrangement (so vessel hog-sag effects need to be taken into account). Four lift points are located on the upper deck. Although the lower level is presumed to be plated, its contribution to the global strength is not considered in the analysis i.e. it is treated as secondary steel.
The overall analysis results at the “Start” of Stage 3 optimization and those after 25 iterations are shown in Figure 3 where it is noted that “grey” indicates member unity check (UC) of less than 75% of capacity. In this case, the “optimization” is downwards ie modelled member weight is reduced as the starting model is found to have conservative design. The grey areas in the after-Stage-3 indicate potential for further optimization.
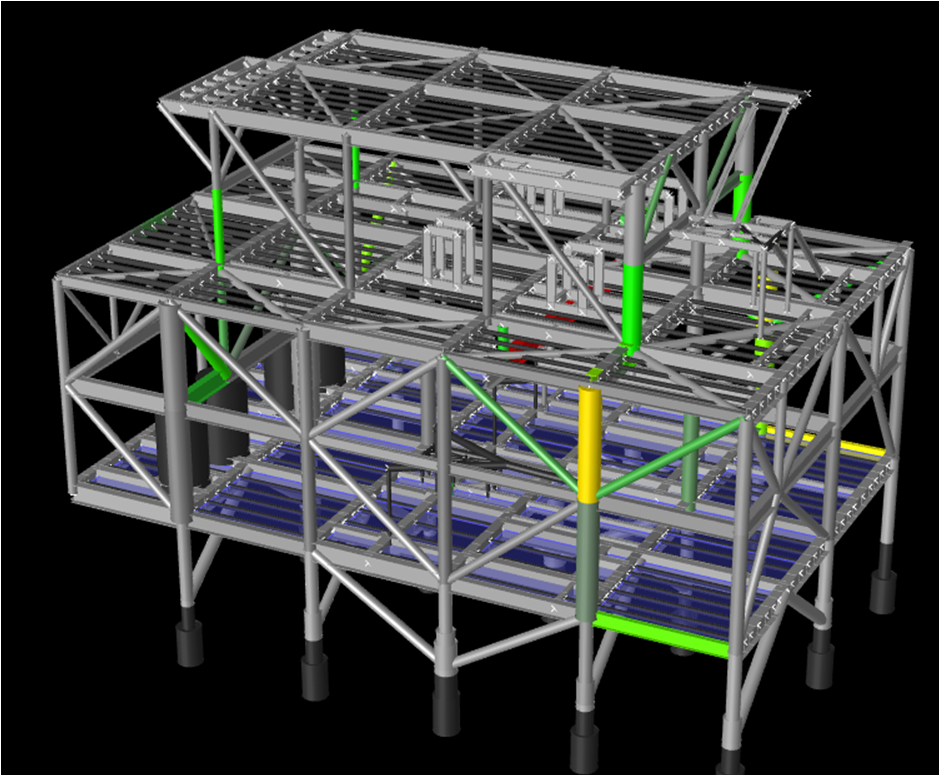
BEFORE (modelled structure weight = 3848 kN) |
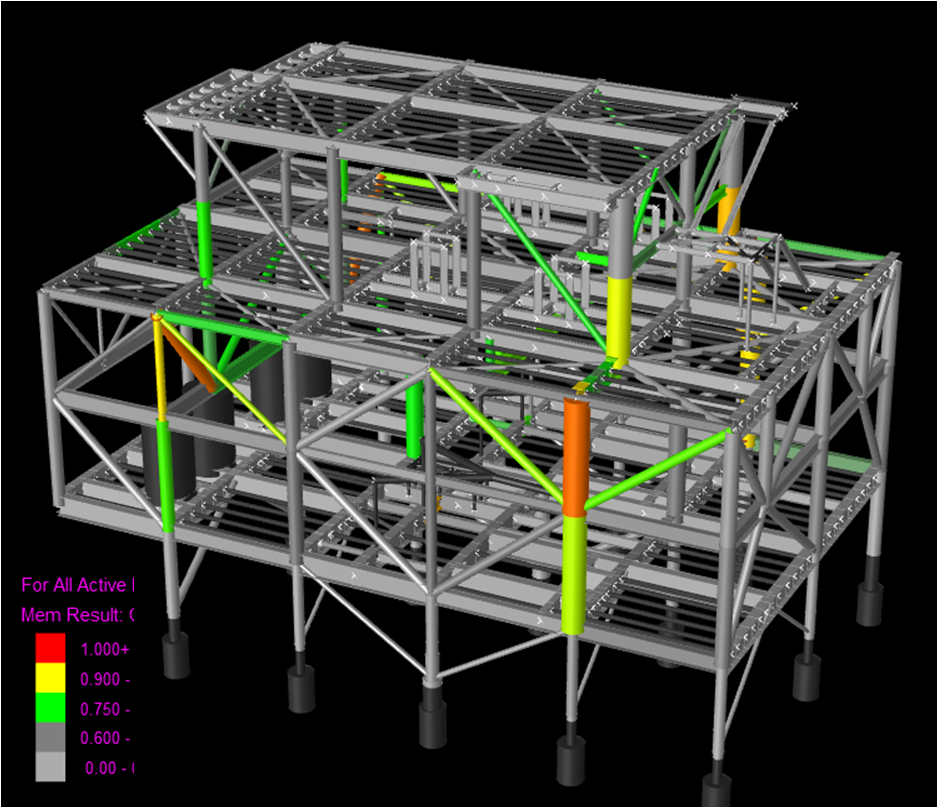
AFTER (modelled structure weight = 3187 kN) |
Figure 3- Module MP3 Strength Analysis Member Unity Check Result BEFORE and AFTER Stage Three Optimization
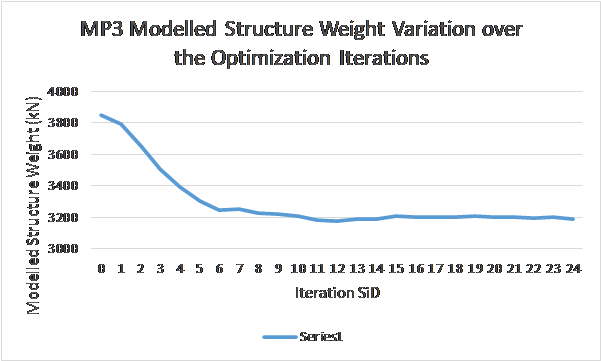
It is noted that the difference in modelled structure weight between the start and end is about 66 MT removed. The progression of modelled weight at each iteration step of optimization process is shown in Figure 4.
Figure 4- MP3 Modelled Structure Weight At Each Optimization Step
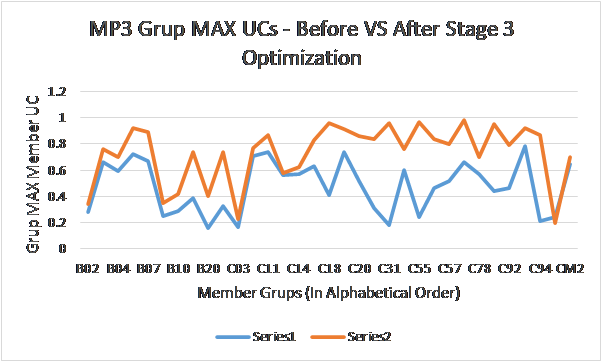
To demonstrate the effectiveness of the optimization strategy, a Before-Vs-After member unity check comparison is presented in Figure 5. The “blue” curve shows the “before Stage 3 optimization” value of the maximum member UC in each active member “Grup”. The “orange/red” curve shows the corresponding “after” value noting that the ideal result would be a horizontal line at UC = target value (which in this case is 1.0). It can be seen that the UC result for each “Grup” has been “steered” toward the target.
Figure 5- MP3 Member Grup Maximum UCs – Before VS After Comparison
1.6.3 Low Pressure Compression Module at Detail Design Status
This model is also based on a relatively mature structural design of a module on a recent FPSO delivery project and is referred to as MS3 here. It was developed by a 3rd Party and adapted here for processing via the standardized analysis workflow employed in the Optim22 method.
The structural framing concept is “post and beam” construction and the support system features four elastomeric supports in a 2×2 (rows) stool arrangement. The four lift points are located on the upper deck with one located on the middle deck corner that is open to the sky. Same as for module MP3, the contribution of the plated lower level is presumed to not contribute to the global strength in the analysis. Other distinguishing features are a stair-tower and a crane boom rest. This model is shown in Figure 8 and total “pre-optimized” dry and operating weight considered was 1700/1900 MT.
Figure 6- SACS model for MS3 Module
The overall analysis results at the “Start” of Stage 3 optimization and after 25 iterations are shown in Figure 7 where it is noted that “grey” indicates a member unity check (UC) of less than 75% of capacity. In this case, the “optimization” is downwards as the starting model has excess capacity. The grey areas in the after-Stage-3 indicate the potential for further optimization. Note that column that appears “red” is actually “orange”.
.
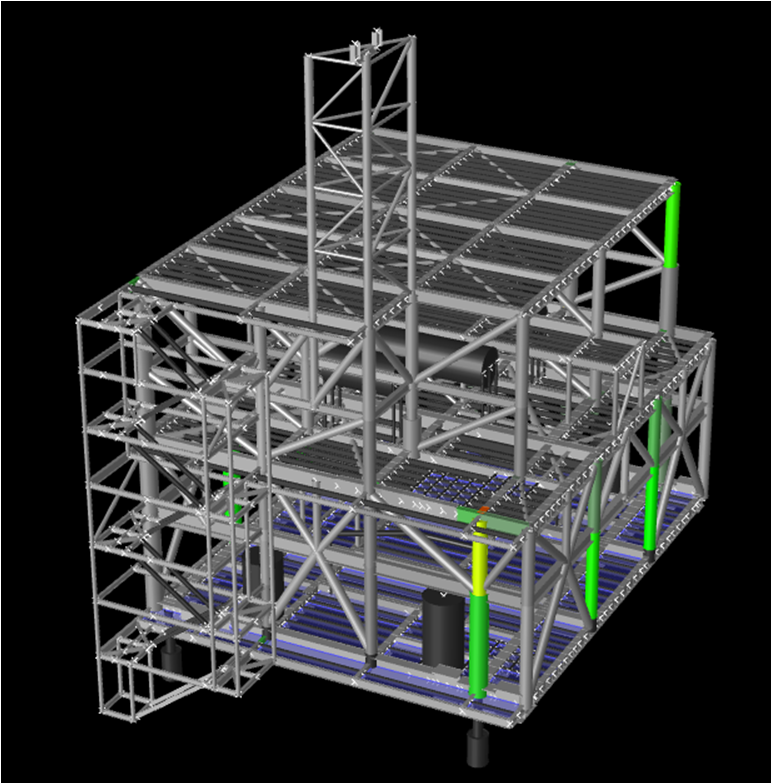
BEFORE (modelled structure weight = 5680 kN) |

AFTER (modelled structure weight = 5260 kN) |
Figure 7- Module MS3 Strength Analysis Member Unity Check Result BEFORE and AFTER Stage Three Optimization
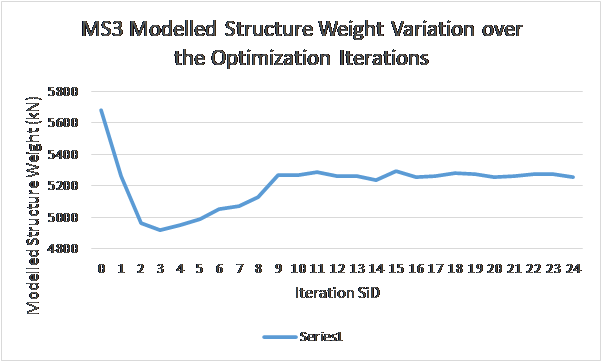
It is noted that the difference in modelled structure weight between the start and end is about 42 MT removed. The progression of modelled weight at each iteration step of optimization process is shown in Figure 4. In this case, the optimization went past the target around iterations 3 and 4 ie introduced some member failures but then corrected and settled down around the 10th iteration.
Figure 8- MS3 Modelled Structure Weight At Each Optimization Step
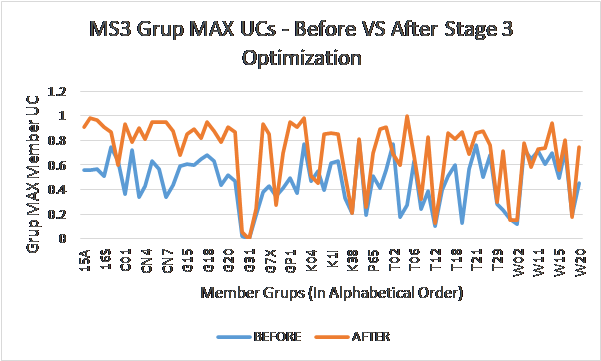
To demonstrate the effectiveness of the optimization strategy, a Before-Vs-After member unity check comparison is presented in Figure 9. As in the MP3 case study, the “blue” curve shows the “before Stage 3 optimization” value of the maximum member UC in each active member “grup” and the “orange/red” curve shows the corresponding “after” value again noting that the ideal result would be a horizontal line at UC = target value (1.0). It can be seen that the UC result for each “grup” has been “steered” toward the target, particularly the underutilized UC values in the “Before” case.
Figure 9- Module MS3 Member Grup Maximum UCs – Before VS After Comparison
1.6.4 Seawater Systems Module at FEED Status
This model served as the basis of the FEED design estimates in a recent FPSO delivery project. It was produced by a TheNavalArch.com team member based on concept phase (Pre-FEED) topsides equipment list, weight report and modules general arrangement. The structural design specification of the Owner’s design contractor was followed with appeal to the analyst’s structural design specification for modelling requirements not covered. It is detailed enough to include deck footprint beams for equipment groups greater than 10 MT.
The module structural analysis model features 5 deck levels (including a mezzanine deck and service platform on top) and the support system is a “elastomeric” system with 3×2 (rows) stool arrangement. Four lift points are located on the upper deck. Although the lower level is presumed to be plated, its contribution to the global strength is not considered in the analysis i.e. it is treated as secondary steel. This model is shown in Figure 10 and total “pre-optimized” dry and operating weight considered was on the order of 1300/1500 MT.
A particular feature of this analysis that demonstrates the versatility of the Optim22 method was to account for the effects of two-step load application during module installation on the FPSO. Ie.
- Initial installation was assumed to be on 4 of supports with only module dry weight present
- 2nd step features addition of the remaining two supports and then application of the remaining loads.
Figure 10- SACS model for MP7 Module
The overall analysis results at the “Start” of Stage 3 optimization and after 25 iterations are shown in Figure 11 where it is noted that “grey” indicates member unity check (UC) of less than 75% of capacity while the spots of “red” indicates members that are failing their design criteria. In this case, the “optimization” is upwards as the starting model featured some member failures. The grey areas in the after-Stage-3 indicate potential for further optimization.
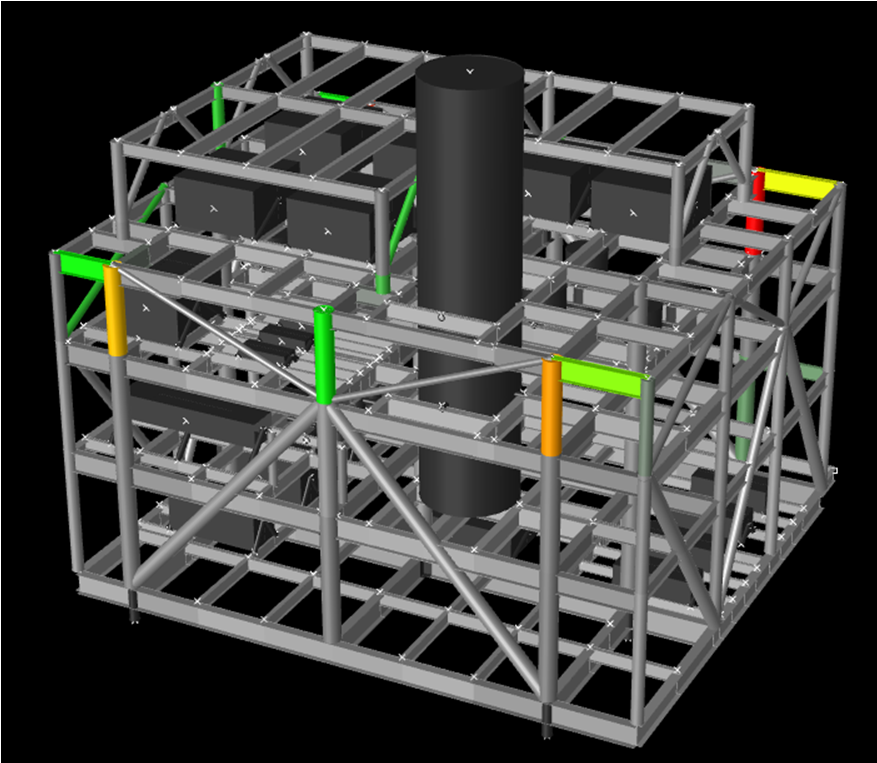
BEFORE (modelled structure weight = 6260 kN) |

AFTER (modelled structure weight = 7900 kN) |
Figure 11- Module MP7 Strength Analysis Member Unity Check Result BEFORE and AFTER Stage Three Optimization
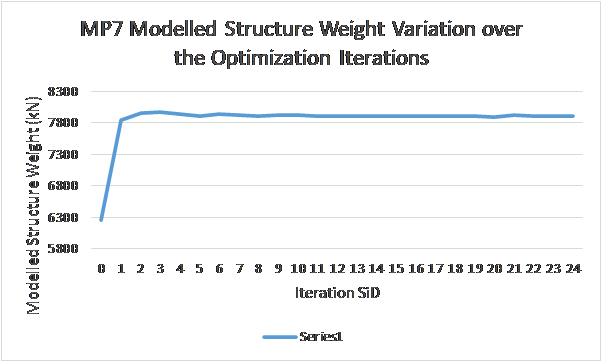
It is noted that the difference in modelled structure weight between the start and end is about 170 MT added. The progression of modelled weight at each iteration step of optimization process is shown in Figure 6. After the 5th iteration, this weight (as well as its CoG location) remained constant so is considered an optimal solution.
Figure 12- MP7 Modelled Structure Weight At Each Optimization Step
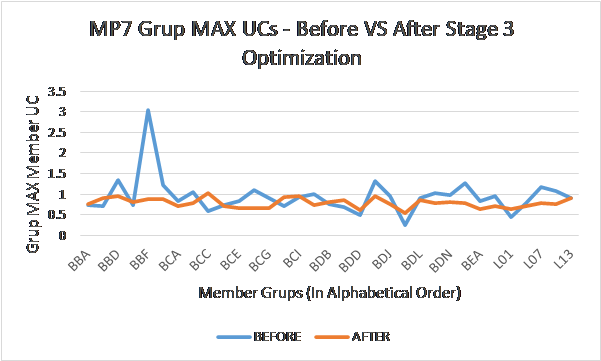
To demonstrate the effectiveness of the optimization strategy, a Before-Vs-After member unity check comparison is presented in Figure 13. The “blue” curve shows the “before Stage 3 optimization” value of the maximum member UC in each active member “Grup” noting that there are several “Grups” featuring overstressed members. The “orange/red” curve shows the corresponding “after” value noting that the ideal result would be a horizontal line at UC = target value (which in this case is 1.0). It can be seen that the UC result for each “Grup” has been “steered” toward the target, particularly the overstressed values in the “Before” case.
Figure 13- MP7 Member Grup Maximum UCs – Before VS After Comparison
1.6.5 Concluding Remarks
- Present implementation. At present the method has been developed for use in conjunction with the SACS structural analysis program. It could be adapted to work with other structural analysis programs that have ascii format input and output files or other “readable” interface data files.
- “Optimized structural design” here means that each component ideally meets its required design capacity with little or none to spare. It is acknowledged that the “ideal” is very difficult to meet 100% of the time.
- Importance of Stage 1 and 2 optimization steps (as presented in the previous article). Lots of “grey” is observed in the UC plots of all the optimized structures presented here. Although the MAX Grup UC’s are steered toward the target, still there are members in many Grups whose UCs are much less than the target. Another way of saying this is that there is a wide range of governing load on members in a given Grup in these Case Studies so it would be beneficial to split some Grups into 2 or more so these part-Grups could be optimized separately.
- Automation of structural analysis execution. This feature has been implemented in the case studies presented in this article where it was not available for the case studies presented in the previous article. Although the Optim22 method can theoretically accommodate runs featuring hundreds of optimization iterations, in practice a limit of 25 iterations is currently set so that mid-sized modules can be put through the Stage 3 optimization process in an overnight time frame.
- The optimization process presented here leads to a minimum weight solution for a given structural configuration. It is intended to provide a starting point for a cost-benefit analysis where constructability considerations are taken into account. The value of minimum weight solutions depends on the cost of installed structural steel and also the relative cost of construction. For example, if material is expensive but labour is relatively cheap, then optimized weight takes on more significance in the overall cost.
- Design schedule. A key selling point for the method described herein is speed of execution. After preparation of the base input model, the optimization process for even very large structural models can be carried out in a few days. This makes it feasible to employ it for Concept and FEED design as well as short-duration design reviews to evaluate multiple structural configurations.
- Quality of results. In the final tally, the procedure just generates input for a structural analysis program so that no intermediate member section parameter estimates are used in isolation in the design. These are always verified for project requirements in the check of the structural analysis program’s input and analysis output.

Michael Harwood
CCnBW at MCHTM Inc
Forward looking, project-oriented engineer and manager with over 30 years design, analysis and work management/coordination experience mainly in the offshore oil and gas industry. Present focus is on providing customers/employers with designs that are optimized for weight and constructability within cost and schedule constraints. Rapid delivery of these is achieved by automating calculation processes as much as possible, particularly when dealing with interface data from mechanical and piping disciplines. Refer to my recent LinkedIn articles for examples.
CAREER OVERVIEW:
Began as a structural engineering analyst out of university and moved up into hands-on management positions both in operations and projects. Acquired overall knowledge of oil and gas production facilities and gained both US and international experience along the way. Familiar with both owner’s and contractor’s interests so can work as Owner’s Engineer or EPC Contractor PMT member. Became an independent consultant in 2008 working and work through MCHTM Inc or as a contract engineer depending upon what works best for my client. Along the way, have worked on approximately 50 projects and 20 tenders of various durations and produced over 1000 report, drawing, and specification deliverables of varying scope.
GOAL: To have satisfied customers/employers
SPECIALTIES
Specialties: Structural engineering subject matter expert. Expert user of structural analysis computer programs and offshore and ship design codes. Also familiar with subsea equipment structures and installation aids as well as offshore pipeline installation equipment and aids. Brown field and newbuild. Structural engineering planning and management.
Design aid software developer to advance design automation, design work methods planner, construction engineering support. Coach/mentor of junior engineers.
General experience with hull and mooring systems and topsides production facilities on the following offshore platform types: FPSOs; CPTs, Spars; Production Semis; TLPs, MODUs; MOPUs and Fixed Base as well as the following ship types: Drilling, S-lay Pipelay; Naval.

TRANSPORT VESSELS FOR FLOATING WIND
By Alan Crowle, BSc, MSc, CEng, CMarEng, FRINA, FMAREST, FSCMS Masters by Researcher, University of Exeter, College of Engineering, Mathematics and Physical Sciences, Renewable Energy Group SUMMARY Floating wind turbine construction is a large logistical exercise. The...

Using simple tools for efficient Passage Planning for seagoing vessels
Introduction Planning a vessel’s voyage is a critical detailed exercise, and the main goal is to ensure safe and efficient passage between two ports. The Master has the responsibility for the vessel voyage planning, but very often he delegates the actual voyage...

Designing a closed chock as per IACS rules
Introduction Chocks are used universally for mooring and towing operations on ships. For towing operations, Chocks are used for guiding the towing rope from the winch through the outer shell of the vessel to the tug. For mooring operations, the chock is used to...

The Optim22 Method of Weight Optimization of Framed Steel Structures
1 Abstract A semi-automated structural weight optimization system is presented for framed structures of post and beam construction which is based on basic structural member design principles. The approach is to adjust member properties in a manner that...
How to identify the spoolpiece lifting points?
In the offshore construction industry, the connection between the newly installed pipeline and the riser is accomplished via a series of ‘spoolpieces’ (or spools). The spool is fabricated by welding pipe joints to form an L-shaped, Z-shaped, or possibly a straight...

Sea Pressure Loads Calculation based on DNV Rules
Introduction Sea pressure loads are an important factor in the structural design of a vessel. What is sea pressure load? As the term suggests, it is the external pressure on the vessel due to the surrounding sea. What kind of pressure it is, and how to...
Designing Fillet Welds for Symmetrical Joint Sections
Introduction Fillet welds are the most commonly used weld types in marine structures. A fillet weld is used when there are two pieces of metal that are joined perpendicular to each other or at an angle. In this article, we will explore how to select the right size...

Designing a stanchion/stopper for sea-fastening of deck cargo
Introduction Stanchions – a familiar term for mariners and ship designers. What are Stanchions? A stanchion is generally a vertical pipe or beam which is used to support some structural item or provide support rails on the deck. In ships, the most common type of...

Global wave statistical analysis and its use in deepwater operations
Why do we need wave analysis? For the design of offshore operations such as installation and transport of offshore structures, as well as lifecycle design of floating and fixed structures, knowledge of extreme waves as well as the probability of different sea-states...
Designing a clip/dog plate for seafastening
Introduction In an earlier article, we saw how to design stoppers for seafastening. Stoppers are items that are used to contain the translation movements (longitudinal and transverse directions) of a cargo on the deck/hold of a vessel. That brings us to the question –...