Introduction
The longitudinal strength of a vessel is integral to its evaluation for a given purpose. To get an introduction to the topic, please refer to our other article
https://thenavalarch.com/longitudinal-strength-ships-introduction/
In this article, we’ll see from a regulatory (Classification) perspective, what the important factors determining Longitudinal Strength requirements for barges are.
Longitudinal Strength determines the global strength characteristics of the Barge. Referring to our previous article, considering the ship as a simply supported beam, the strength will depend on the strength of the structural cross-section of the ship. Most of the time, the midship structural section is considered the representative for the barge’s strength as the maximum bending moment is expected at midship.
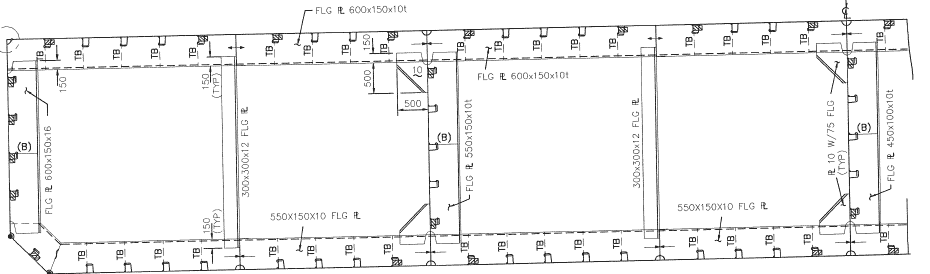
A midship section of a Barge is shown below:
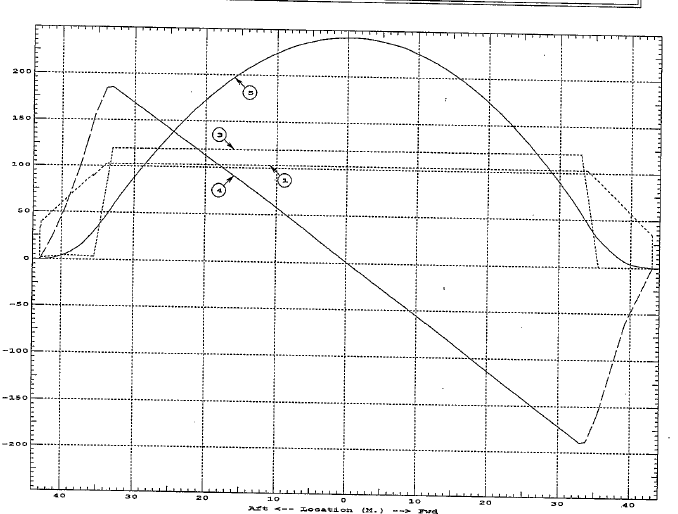
Also, a typical bending moment diagram of a barge is shown below:
We can see that the midship section is the critical one since the bending moment amidships is the largest
What parameter determines the strength of the midship section of the Barge?
Beam analogy
Considering the beam analogy, the strength of the beam depends upon the section property of the beam. In short, the bending stress on the beam is given by:
Bending Stress = Bending Moment/Section Modulus
Thus, the defining parameter that dictates the beam’s strength is its Section Modulus.
How do we calculate the Section Modulus of the midship section (or any other section) of the ship?
The calculation of section modulus is investigated in another related article:
https://thenavalarch.com/how-to-calculate-the-strength-of-midship-section-of-a-ship/
The role of Classification Rules
Once we have calculated the section modulus of the midship section of the Barge, how do we know if it is sufficient? How do we know what should be the minimum section modulus for the Barge to be fit to ply in the open ocean?
The requirements for minimum strength characteristics are provided by regulatory bodies (a.k.a. Classification Societies like ABS, DNV, LR, IRS, CCS, etc.)
In this article, we’ll see from a regulatory perspective (i.e., Ship Classification) the requirements for longitudinal strengths of Barges.
We will refer to the American Bureau of Shipping (ABS) Rules for Building and Classing Steel Barges, 2020 for this article. It is to be noted that these rules apply to ocean-going barges with a Breadth-to-Depth ratio of up to 4.
The Classification rules help by providing the minimum requirements that the vessel must meet.
With regard to the longitudinal strength of Barges, the two important parameters that the rules have laid out are:
- Minimum Section Modulus amidships
- Minimum Hull girder moment of Inertia amidships
Minimum Section Modulus amidships
The minimum section modulus requirement is specified in the American Bureau of Shipping (ABS) Rules for Building and Classing Steel Barges, 2020, Part 3, Ch.2, Section 1, 3.1
The required Section Modulus amidships (SMR) is given by
SMR = K SMb
where
SMb = C1C2L2B (Cb + 0.7) cm2-m (in2-ft)
- C1 is a coefficient dependent of the length of the barge, and is higher or longer vessels
- C2 is a constant (0.01)
- K = 0.629 + Ms/(fp SMb) but is not to be taken less than 1.0
Ms = maximum still-water bending moment in the governing loaded or ballasted condition in kN-m (tf-m, Ltf-ft). When still-water bending moment calculations are not submitted, K will be taken as 1.0.
- fp = 17.5 kN/cm2(1.784 tf/cm2, 11.33 Ltf/in2)
The factor K
As highlighted earlier, the bending stress on the midship section is given by
Bending Stress = Bending Moment / Section Modulus
Putting it the other way round,
Section Modulus = Bending Moment/Bending Stress
Thus, if we know the maximum bending moment that the vessel experiences and we know the limit of the bending stress of the material used, we can find out the minimum section modulus that the vessel requires.
The maximum still water bending moment that the vessel experiences can be obtained from the stability booklet, in which the full-load and ballast conditions, including any additional condition (critical in terms of long strength), are included. The highest still water bending moment of all these conditions is used for the calculation of K. When bending moment calculations are not available, K is to be taken as 1.
The still water bending moment (SWBM) calculations are mandatorily required to be submitted if the Barge is of length 76 m or more.
fp is simply the allowable bending stress of the material used and translates to 175 MPa for mild steel, which is 75% of the yield strength of steel.
Minimum Section Modulus amidships
The moment of inertia amidships is derived from the required section modulus, and is given by (Ref [1], 3-2-1, Sec 5):
I = 0.03SMRL cm2-m2 (in2-ft2)
where
L = length of the barge as defined in 3-1-1/3
SMR = hull girder section modulus required for the barge per 3-2-1/3.1, in cm2-m (in2-ft)
High Strength Material
The above rules are applicable to the case when the hull material is Mild Steel. If high strength materials are used for either the upper or lower flanges of the hull girder or both, then a reduction factor is used in the calculation of the required Section Modulus (Ref [1], 3-2-1, Sec 11.3):
SMhts = Q (SMR)
where
Q = 0.78 for H32 strength steel
Q = 0.72 for H36 strength steel
H32, H36 = as specified in Section 2-1-3 of the ABS Rules for Materials and Welding (Part 2)
Wave Bending Moment
Besides the still water bending moment, the vessel also experiences Wave Bending moment in seas. The wave bending moment is considered when there are additional buckling calculations to be submitted to verify the scantlings of the vessel. To account for the wave bending moment in calculations of the factor K, the bending moment used is
Bending moment = Still Water Bending Moment + Wave Bending Moment
The formula used for wave bending moment is
Wave bending moment = Sw x SMb, where Sw = 11.0 kN/cm2, or 110 MPa.
Considering the above, the formula for K becomes
K = 0.629 + (Sw x SMb + MS)/(fp x SMb) = 0.629 + {Sw/fp + Ms/(fp x SMb)}
Thus, it is important to calculate the K factor accurately in order to get a reliable value for the required section modulus for the vessel.
That sums up this article about using Class rules to assess the longitudinal strength of Barges. The required section modulus is an important starting point to design the structural section of the vessel by selecting the right strength elements.
References
[1] ABS RULES FOR BUILDING AND CLASSING STEEL BARGES, JULY 2020
[2] ABS Rules for Materials and Welding (Part 2), July 2020
Disclaimer: This post is not meant to be authoritative writing on the topic presented. thenavalarch bears no responsibility for the accuracy of this article, or for any incidents/losses arising due to the use of the information in this article in any operation. It is recommended to seek professional advice before executing any activity which draws on information mentioned in this post. All the figures, drawings, and pictures are property of thenavalarch except where indicated, and may not be copied or distributed without permission.
TheNavalArch Interview Series: Mr. Balakrishna Menon
Mr. Balakrishna MenonEngineering Director Mooreast (Asia) Pte Ltd TheNavalArch's Interview Series is an endeavor to get insights from the best engineering and business brains in the industry, and present them to its users for the larger...

Floating Rice Fields, the quest for solutions to combat drought floods and rising sea levels
by Lim Soon Heng, BE, PE, FSSS, FIMarEST Founder President, Society of FLOATING SOLUTIONS (Singapore) Abstract Amazing as it seems, there is a case for growing rice on floating platforms in the sea. The capital expenditure to develop this is offset by the opportunity...

CAPSIZE OF LIFTBOAT IN TRANSIT
This paper was originally presented in the 27th Offshore Symposium, February 22nd, 2022, Houston, Texas Texas Section of the Society of Naval Architects and Marine Engineers It has been reproduced here for the readers of TheNavalarch INTRODUCTION In 1989 a Class 105...

Designing a closed chock as per IACS rules
Introduction Chocks are used universally for mooring and towing operations on ships. For towing operations, Chocks are used for guiding the towing rope from the winch through the outer shell of the vessel to the tug. For mooring operations, the chock is used to...
The Optim22 method of hull optimization – Part 2
This is a follow-up article to the previous article on Framed Structures Optimization. 1.1 Abstract A previous article introduced the Optim22 method. This one adds additional background information plus 3 more case studies to...

The Optim22 Method of Weight Optimization of Framed Steel Structures
1 Abstract A semi-automated structural weight optimization system is presented for framed structures of post and beam construction which is based on basic structural member design principles. The approach is to adjust member properties in a manner that...

Combating rising seas with floating structures
Introduction Rising sea level is an existential threat for many coastal cities. The sea is rising subtly but relentlessly at an exponential rate. Many predictions of how high and how fast it will rise in the next 50 years have proved to be understated. According to...

Sea Pressure Loads Calculation based on DNV Rules
Introduction Sea pressure loads are an important factor in the structural design of a vessel. What is sea pressure load? As the term suggests, it is the external pressure on the vessel due to the surrounding sea. What kind of pressure it is, and how to...

A quick empirical method for resistance estimation of planing vessels
Resistance estimation for a vessel is a fundamental exercise in design of the vessel. Resistance is a property that depends on the vessel’s shape and form. A conventional ship-shaped vessel with a bulb will have completely different resistance characteristics compared...

Powering the maritime industry with Hydrogen – Part 2
Powering the shipping industry with hydrogen - Part 2: Hydrogen propulsion on a ship - opportunities and challenges Introduction In the Part 1 of this article, we explored the basic properties of Hydrogen as a fuel, and also the opportunities and challenges...




Nice content. There is need to understand the first principles first to appreciate every parameter and models highlighted in this article. Thank you for putting this together.